Original Article:
"http://people.math.gatech.edu/~thomas/FC/fourcolor.html"
Esta página es un breve resumen de una nueva prueba del Teorema de los Cuatro Colores y un algoritmo de cuatro colores descubierto por Neil Robertson, Daniel P. Sanders, Paul Seymour y Robin Thomas.
Índice:
1) Historia.
2) ¿Por qué es una nueva prueba?
3) Esquema de la prueba.
4) Características principales de nuestra prueba.
5) Configuraciones.
6) Reglas de descarga.
7) Punteros.
8) Un algoritmo cuadrático.
9) Discusión.
10) Referencias.
Historia.
El problema de los cuatro colores se remonta al año 1852 cuando Francis Guthrie observó que los cuatro colores eran suficientes al tratar de colorear el mapa de los condados de Inglaterra. Le preguntó a su hermano Frederick si era cierto que cualquier mapa puede ser coloreado usando cuatro colores de tal manera que las regiones adyacentes (es decir, aquellas que comparten un segmento fronterizo común y no solo un punto) reciben diferentes colores. Frederick Guthrie entonces comunicó la conjetura a DeMorgan. La primera referencia impresa apareció en 1878 gracias a Cayley.
Un año más tarde apareció la primera "prueba" de Kempe; las incorrecciones fueron señaladas por Heawood once años más tarde. Otra prueba fallida ocurrió gracias a Tait en 1880; un vacío en el argumento fue señalada por Petersen en 1891. Sin embargo, ambas pruebas fallidas tenían cierto valor. Kempe descubrió lo que se conoció como cadenas de Kempe, y Tait descubrió una formulación equivalente del Teorema de los Cuatro Colores en términos de coloración de 3 bordes.
La siguiente contribución importante vino gracias a Birkhoff, cuyo trabajo permitió a Franklin demostrar que la conjetura de cuatro colores es verdadera para mapas con un máximo de 25 regiones en el año 1922. También fue utilizado por otros matemáticos para hacer varias formas de progreso en el problema de los cuatro colores. Hace falta mencionar la persona llamada Heesch, quien desarrolló los dos ingredientes principales necesarios para la prueba definitiva: reducibilidad y descarga. Mientras que el concepto de reducibilidad fue estudiado por otros investigadores también, parece que la idea de descarga, crucial para la parte inevitable de la prueba ocurrió gracias a Heesch, y que fue él quien conjeturó que un desarrollo adecuado de este método se encontraba en la soción del problema de los cuatro colores.
Esto fue confirmado por Appel y Haken en el año 1976, cuando publicaron su prueba del Teorema de los Cuatro Colores. [1.2]
¿Por qué es una nueva prueba?
Existen dos razones por las cuales la prueba de Appel-Haken no es completamente satisfactoria.
• Parte de la prueba de Appel-Haken utiliza una computadora, y no se puede verificar a mano, y
• incluso la parte que supuestamente es a mano chequeable es extraordinariamente complicado y tedioso, y hasta donde sabemos nadie lo ha verificado en su totalidad.
En realidad hemos intentado verificar la prueba de Appel-Haken, pero pronto nos dimos por vencidos. Comprobando la parte de la computadora no sólo requeriría mucha programación, sino también la introducción de las descripciones de 1476 gráficos, y que ni siquiera era la parte más polémica de la prueba.
Decidimos que sería más rentable elaborar nuestra propia prueba. Así que lo hicimos y surgió una prueba y un algoritmo que se describen a continuación.
Esquema de la prueba.
La idea principal de la prueba es la misma que la de Appel y Haken. Exponemos un conjunto de 633 "configuraciones", y demostramos que cada una de ellas es "reducible". Este es un concepto técnico implicando que ninguna configuración con esta propiedad puede aparecer en un contraejemplo mínimo al Teorema de los Cuatro Colores. También puede usarse en un algoritmo, ya que si una configuración reducible aparece en un grafo plano de G’, entonces se puede construir en tiempo constante un grafo plano menor G’ tal que cualquier cuatro colorantes de G' pueden convertirse en G’ en tiempo lineal.
Se ha conocido desde 1913 que cada contraejemplo mínimo para el Teorema de los Cuatro Colores es una triangulación internamente con 6 conectores. En la segunda parte de la demostración probamos que al menos una de nuestras 633 configuraciones aparece en cada triangulación planar internamente con 6 conectores (y no necesariamente un contraejemplo mínimo para el 4CT). Esto se llama prueba de la inevitabilidad, y utiliza el "método de descarga", sugerido por Heesch por primera vez. En este mismo aspecto nuestro método difieredel de Appel y Haken.
Características principales de nuestra prueba.
Confirmamos la conjetura de Heesch en que se puede encontrar una configuración reducible en el segundo vecindario de un vértice sobrecargado; Así evitamos los problemas de "inmersión" que fueron una fuente importante de complicaciones para Appel y Haken. Nuestro conjunto inevitable tiene el tamaño 633 en comparación con el conjunto de 1476 miembros de Appel y Haken, y nuestro método de descarga utiliza sólo 32 reglas de descarga, en lugar de los 300+ de Appel y Haken. Finalmente, se obtiene un algoritmo cuadrático para graficas planares de los cuatro colores (descritas a continuación), una mejora sobre el algoritmo cuártico de Appel y Haken.
Configuraciones.
Una triangulación cercana es un gráfico de plano sinóptico conectado no nulo de tal manera que cada región finita es un triángulo. Una configuración K consiste en una triangulación cercana de G y un mapa g de V (G) a los enteros con las siguientes propiedades:
1. Para cada vértice v, G \ v tiene dos componentes como máximo, y si hay dos, entonces el grado de v será g (v) -2,
2. Para cada vértice v, si v no es incidente con la región infinita, g (v) es igual al grado de v, y de otra forma g (v) es mayor que el grado de v; Y en cualquier caso g (v)> 4,
3. K tiene al menos un tamaño 2 de anillo, donde el tamaño de anillo de K se define como la suma de g (v) -deg (v) -1, sumado sobre todos los vértices v incidentes con la región infinita tal que G \ v está conectado.
Cuando dibujamos imágenes de configuraciones utilizamos una convención introducida por Heesch. Las formas de vértices indican el valor de g (v) de tal manera: un círculo negro sólido significa g (v) = 5, un punto (o lo que aparece en la imagen como ningún símbolo en absoluto) significa g (v) = 6, un círculo hueco significa g (v) = 7, un cuadrado hueco significa g (v) = 8, un triángulo significa g (v) = 9 y un pentágono significa g (v) = 10. (No necesitamos vértices v con g (v)> 11, y sólo un vértice con g (v) = 11, para lo cual no usamos ningún símbolo especial.) En la imagen abajo los 17 de nuestras 633 configuraciones reducibles se muestran tilizando la convención indicada. El conjunto completo se puede ver haciendo clic aquí. (Nos referimos a (3.2) de nuestro papel [7] para el significado de "bordes gruesos" y "bordes bordes" en esas imágenes.)
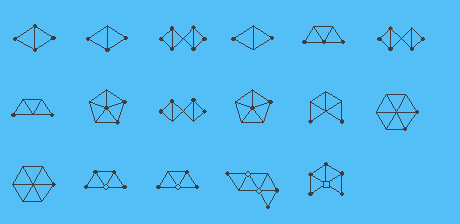
Cualquier configuración isomorfa a una de las 633 configuraciones mostradas en [7] se llama una buena configuración. Que sea T una triangulación. Una configuración K = (G, g) aparece en T si G es un subgrafo inducido de T, toda región finita de G es una región de T, y g (v) es igual al grado de v en T para cada vértice v de G. Podemos probar dos siguientes afirmaciones.
TEOREMA 1. Si T es un contraejemplo mínimo para el Teorema de los Cuatro Colores, entonces ninguna buena configuración aparece en T.
TEOREMA 2. Para cada triangulación T conectada internamente, una buena configuración aparece en T.
De los dos teoremas anteriores se deduce que no existe ningún contraejemplo mínimo, por lo que el 4CT es verdadero. La primera prueba necesita una computadora. El segundo se puede comprobar manualmente en unos pocos meses, o, utilizando un ordenador, se puede verificar en unos 20 minutos.
Reglas de descarga.
Que sea T una triangulación internamente con 6 conectores. Inicialmente, a cada vértice v se le asigna una carga de 10 (6-deg (v)). De la fórmula de Euler se deduce que la suma de las cargas de todos los vértices es 120; En particular, es positivo. Ahora redistribuimos las descargas de acuerdo con las siguientes reglas. Siempre que T tiene un subgrafo isomorfo a uno de los gráficos de la figura siguiente que satisface las especificaciones de grados (para un vértice v de una regla con un signo menos al lado de v esto significa que el grado del vértice correspondiente de T es el valor especificado por la forma de v como máximo, y de manera análoga para los vértices con un signo más junto a ellos se requiere igualdad para los vértices sin signo al lado de ellos) se enviará una descarga de uno (dos en el caso de la primera regla) a lo largo de la borde marcado con una flecha.
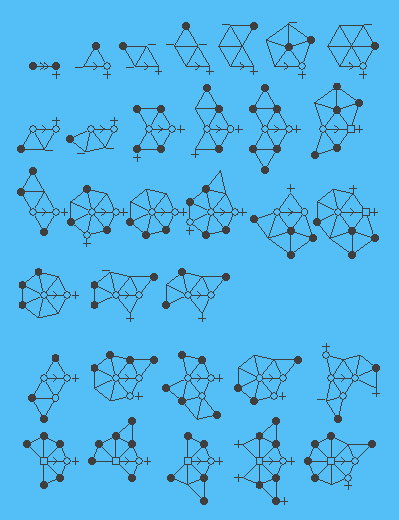
Este procedimiento define un nuevo conjunto de descargas con la misma suma total. Puesto que la suma total es positiva, hay un vértice v en T cuya nueva descarga es positiva. Con este mostramos que una buena configuración aparece en el segundo vecindario de v.
Si el grado de v es 6 máximo o 12 mínimo, entonces esto puede ser visto por un argumento directo. Para los casos restantes, las pruebas son mucho más complicadas, sin embargo. Por lo tanto, hemos escrito las pruebas en un lenguaje formal para que puedan ser verificadas por una computadora. Cada paso individual de estas pruebas es humano-verificable, pero las pruebas en sí no son realmente verificables a mano debido a su longitud.
Punteros.
La parte teórica de nuestra prueba se describe en [7]. Una encuesta de 10 páginas está disponible on-line. Los datos de la computadora y los programas suelen estar ubicados en un servidor ftp anónimo, pero ese servidor ya se ha eliminado. Los mismos archivos están actualmente disponibles en http://www.math.gatech.edu/~thomas/OLDFTP/four/ y pueden ser vistos convenientemente. Un conjunto independiente de programas fue escrito por Gasper Fijavz bajo la dirección de Bojan Mohar.
Un algoritmo cuadrático.
La entrada al algoritmo será una triangulación plana G con n vértices. (Esto no incluye la pérdida de generalidad, ya que cualquier gráfico plano puede ser triangulado en tiempo lineal.) La salida será una coloración de los vértices de G con cuatro colores.
Si G tiene cuatro vértices como máximo, entonces colorea cada vértice de un color diferente. De lo contrario si G tiene un vértice x de grado k <5, entonces el circuito C que lo rodea es un `k-ring '. Vaya al análisis de k-ring a continuación. De lo contrario G tiene grado cinco mínimo. Para cada vértice calculamos su descarga como se ha explicado anteriormente, y hallamos un vértice v de descarga positiva.
Se deduce de nuestra demostración del Teorema 2 que ambas: una buena configuración aparece en el segundo vecindario de v (en que caso que se puede encontrar en tiempo lineal), o un anillo k que viola la definición de 6 conectores interna se puede encontrar en Tiempo lineal. En este último caso vamos al análisis de los anillos k a continuación, en el primer caso aplicamos la recursión a un cierto gráfico más pequeño. Un cuatro coloración de G puede ser construido a partir de los cuatro colores de este gráfico menor en tiempo lineal.
Dando que un k-ring R está violando la definición de 6 conexiones internas se puede usar un procedimiento desarrollado por Birkhoff. Aplicamos la recursión a dos subgrafos cuidadosamente seleccionados de G. Un cuatro colorante de G puede ser construido a partir de los cuatro colores de los dos gráficos más pequeños en tiempo lineal.
Discusión.
Hace falta mencionar que ambos programas usan sólo aritmética entera, por lo que no necesitamos preocuparnos por los errores de redondeo y los peligros similares de la aritmética de punto flotante. Sin embargo, se puede argumentar que nuestra "prueba" no es una prueba en el sentido tradicional, porque contiene pasos que nunca pueden ser verificados por los seres humanos. En particular, no hemos demostrado la corrección del compilador en el que hemos compilado nuestros programas, ni hemos probado la infalibilidad del hardware en el que ejecutamos nuestros programas. Estos tienen que ser tomados en la fe, y son concebiblemente una fuente de error. Sin embargo, desde un punto de vista práctico, la probabilidad de un error de computadora que aparece consistentemente exactamente de la misma manera en todas las ejecuciones de nuestros programas en todos los compiladores en todos los sistemas operativos en los que se ejecutan nuestros programas es infinitamente pequeño comparado con la probabilidad de un error humano durante la misma cantidad de comprobación de casos. Aparte de esta posibilidad hipotética de que una computadora dé consistentemente una respuesta incorrecta, el resto de nuestra prueba puede ser verificada de la misma manera que las pruebas matemáticas tradicionales. Admitimos que la verificación de un programa de computadora es mucho más difícil que comprobar una prueba matemática de la misma longitud.
Reconocimientos.
Estamos en deuda con Thomas Fowler, Christopher Carl Heckman y Barrett Walls por su ayuda de preparación de esta página. Nuestro trabajo fue parcialmente apoyado por la National Science Foundation.
Referencias.
- - K. Appel and W. Haken, Every planar map is four colorable. Part I. Discharging, Illinois J. Math. 21 (1977), 429-490.
- - K. Appel, W. Haken and J. Koch, Every planar map is four colorable. Part II. Reducibility, Illinois J. Math. 21 (1977), 491--567.
- - K. Appel and W. Haken, Every planar map is four colorable, Contemporary Math. 98 (1989).
- - G. D. Birkhoff, The reducibility of maps, Amer. J. Math. 35 (1913), 114-128.
- - H. Heesch, Untersuchungen zum Vierfarbenproblem, Hochschulskriptum 810/a/b, Bibliographisches Institut, Mannheim 1969.
- - A. B. Kempe, On the geographical problem of the four colors, Amer. J. Math., 2 (1879), 193-200.
- - N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, The four colour theorem, J. Combin. Theory Ser. B. 70 (1997), 2-44.
- - N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, A new proof of the four colour theorem, Electron. Res. Announc. Amer. Math. Soc. 2 (1996), 17-25 (electronic).
- - T.L. Saaty, Thirteen colorful variations on Guthrie's four-color conjecture, Amer. Math. Monthly 79 (1972), 2-43.
- - T.L. Saaty and P. C. Kainen, The four-color problem. Assaults and conquest, Dover Publications, New York 1986.
- - P. G. Tait, Note on a theorem in geometry of position, Trans. Roy. Soc. Edinburgh 29 (1880), 657-660.
- - H. Whitney and W. T. Tutte, Kempe chains and the four colour problem'', in Studies in Graph Theory, Part II (ed. D. R. Fulkerson), Math. Assoc. of America, 1975, 378-413.